SOVIET VOROSHILOV ACADEMY LECTURES
HANDBOOK

By its nature engineer work lends itself to development of numerical standards for requirements in quantities of supplies, equipment, and manpower. Norms for standard engineer construction work are contained in various Soviet handbooks. Formulas for calculating engineer requirements for such operational support as clearing routes of obstacles are discussed in Soviet journals. Rather than repeat all this information here, this section contains information of engineer planning found in the less readily available lectures given at the Soviet Academy of the General Staff (Voroshilov) in the 1970's.

Norms for engineer planning

Engineer Organizations

The engineer units and sub-units of an army include the following:
----- combat engineer regiment;
----- engineer-road and bridge construction regiment;
----- pontoon-bridge regiment;
----- assault crossing battalion;
----- engineer obstacle battalion;
----- engineer company of the command post;
----- engineer recovery and repair company;
----- engineer company of the rear.

For reinforcement, an army can receive the following units and sub-units from higher headquarters:
----- pontoon-bridge regiment or battalion;
----- assault crossing battalion;
----- 1-2 combat engineer battalion;
----- 1-2 engineer road and bridge battalion;
----- separate engineer obstacle clearing battalion.

Engineer units of a front include the following:
----- 1 engineer road and bridge brigade, which can include 3 engineer bridge battalions, 3 engineer road battalions, and one engineer reconnaissance company;
----- 1 combat engineer regiment, which can include 1 engineer reconnaissance company, 1 engineer camouflage company, 1 engineer position (fortification) battalion, and 3 combat engineer battalions;
----- 1-2 pontoon-bridge regiments;
----- 1 separate engineer maskirovka battalion, which can include 2 engineer camouflage companies, 1 engineer technical company, one antiradio camouflage platoon;
----- 1 assault crossing battalion;
----- 1 separate engineer obstacle clearing battalion;
----- 1 separate engineer obstacle battalion;
----- 1 separate engineer battalion to construct the command post;
----- 2-3 separate engineer repair battalions;
----- 1-2 separate engineer assembly parts company (inzhenernaia rota agregatov);
----- 1 engineer company of the rear command post.

For reinforcement a front may receive the following units and sub units:
----- 2-3 engineer bridge regiments;
----- 2-3 pontoon bridge brigades;
----- 2-3 engineer road and bridge construction brigades or regiments;
----- 2-3 combat engineer brigades or regiments.

The front troops can have the following bridging equipment:
----- PMP - pontoon-bridge park) - 11-12 sets;
----- PTS - amphibious transport means) - 210-260;
----- GSP - self-propelled tracked amphibious vehicle) - 110.

The engineer company for road construction and repair in one hour can open a trail or path for deployment of advancing units of 8 -10 kms length. This is in the nature of a rough, tank trail accross country in average terrain. Thus, the engineer road construction and repair regiment of army or front in 10 hrs can open column routes of 150-300 kms total length for the deployment of units, with each engineer company working independently.

A combat engineer regiment of an army, is normally attached to a first echelon division on the main axis. In the course of one night, the regiment can create 54 lanes in mine fields. In 10 hours' work, the regiment can construct 150-300 kilometers of column path. The regiment, in 10 hours' work, can dig out 30-35 kilometers of personnel trenches. In 10 hours' work the regiment can dig out 250-300 emplacements for tanks and combat vehicles.
The engineer road and bridge construction regiment of an army prepares "rokads" (lateral routes of communication parallel to the front) and main supply routes for the army. In 10 hours the regiment can, by its road construction battalions, repair 120-200 kilometers of road or establish 160-300 kilometers of column path.

In an army defensive operation, as a rule, the following roads are established:
----- main supply routes in an army, as a rule, are laid to the front, one road per first echelon division;
----- rokads are laid normally connecting the rear services of the first echelon regiments, a second road connecting the area of the rear services of the first echelon divisions, and a third road connecting the rear services of the army with its adjacents. A rokad is also established along a water obstacle.
----- roads for conducting counter-strikes are also prepared in advance, one road for each of the regiments participating in the counter-strike.

To carry out engineer work of the first priority order, 4-6 hours are needed (in the defense); for carrying out engineer work of the second order on the scale of a division 4 days, an army, 4-6 days are needed. For the organization of a complete defense on the scale of a front, 8-10 days are needed. First priority engineer fortification work includes the following activities, which should be accomplished in 4-6 hours at the small unit level: digging individual foxholes and squad trenches, positions for crew-served weapons, cover for tanks and APC's, laying mine fields, building covered command posts, medical posts, observation posts, preparation of firing lines for AT weapons, preparation of water points, and similar activities. Second order engineer work is essentially everything else that can be done to improve the position, such as: communication trenches, alternate positions, switch positions, bunkers and larger dugouts, mine fields on flanks and other areas, strengthened artillery positions, more elaborate command posts, routes for counterattack and maneuver, positions for defense for reserves and second-echelons, maskirovka, preparation of demolitions and fougass, etc.

The army engineer obstacle battalion is normally used as part of the army mobile obstacle detachment. The battalion can lay a set of 3600 anti-tank mines over a length of 5 kilometers. In two hours, 18 sets of controlled field mines can be laid on up to 2 kilometers of front.

An engineer company of construction of army rear command post can, in a 24 hour period, produce 6,000 cubic meters of work.

One bridge construction company is designated for building under-water bridges.



Engineer equipment

PMZ (as in PMZ-4) means trailered minelayer (pritsepnyi minnyi zagraditel'). The basic load is 200 mines, and the crew consists of 5 men. The time for laying one basic load is 15-20 minutes; the time for reloading 10-15 minutes. The crew can mine 800 meters- l kilometer with one basic load. Three vehicles together are used for the mining. The transport speed is up to 40 km/hr, and the speed of mining is 4-6 kilometers per hour.

There are three vehicles in an engineer company of a motorized rifle or tank regiment and in an engineer mine laying battalion there are 18 vehicles. In an engineer battalion of the division there are 3 vehicles.
Tactical and technical characteristics of the BTM - high speed trencher): There are 2 BTM in a division engineer battalion, 9 in each fortification battalion of the combat engineer regiments of an army and front. The vehicle can dig, in one hour of operation, 300-400 meters of trenches at a depth of 1 meter 10 centimeters. The running distance on one fueling is 500 kilometers; the running on tracks is 3,500 kilometers (in terms of track life). The speed is 35 km/hr. The weight of the vehicle is 27 tons.

A self-propelled, tracked amphibious vehicle (GSP - gusenichnaia samohodnaia plavaiushchaia mashina) is designated to ferry tanks. It can ferry loads of up to 52 tons. On highways, the speed of movement is 40 kilometers per hour, and in water it is 8-10 km/hour. As part of the assault crossing company of an engineer battalion of the division; there are three of these vehicles; there are 20 of these vehicles in an assault crossing battalion of an army.



Crossing water obstacles

In many theaters of military operations the ground forces will be required to conduct crossings over water obstacles frequently. These include rivers, lakes, canals, bays, and flooded areas. Experience shows that the troops will encounter small rivers after each 35 to 60 km of advance, medium rivers every 100-150 km., and wider rivers every 250-300 km. The decision to cross a small river (60 meters wide) is made by the division level (medium by army and wider by front). Therefore, the divisions might have to make a river crossing once a day or sometimes once in two days. In the Western TVD all these rivers flow from the south to the north.
The swimming capabilities of modern APC's and BMP's and the introduction of self-propelled crossing vehicles (GSP) and rapidly constructed bridges enable the troops to conduct a crossing operation in a shorter and more effective way than in the past. The experiences of exercises and tactical norms indicate that the time for the actual crossing (not counting combat prior to the crossing) will be as follows:
----- battalions 1-1.5 hrs.
----- forward detachments of division 2-2.5 hrs
----- first echelon regiments 2-3 hrs
----- first echelon divisions 5-7 hrs
----- first echelon army 12-15 hrs.

In order to conduct a crossing of a water obstacle a division establishes the following crossings:
----- 4-6 assault crossing sites (1-2 for each first echelon battalion;
----- 4-6 raft crossing sites (1 for each tank subunit);
----- three to five under water crossing sites for tanks;
----- 1 bridge for the division.

In the division crossing company there are three GSP's (self-propelled crossing vehicles) which can cross tanks or artillery with their towing vehicles. In the divisional engineer battalion there is a half park of PMP (pontoon bridge) consisting of 18 vehicles. Moreover, the army has two PMP parks in its engineer regiment and 20 GSP's in its assault crossing battalion. During the crossing the army will reenforce the division with crossing equipment.

The experiences of exercises show that missions assigned to regiments for crossing should be issued not later than 1.5-2 hours before the crossing and to battalions not later to 1-1.5 hours before the crossing. In other words regiments receive missions when they are 10-15 km away from reaching the river and battalions 5-8 km before the river. During the pursuit these distances are much longer.

The forward detachment moves in a column led by tanks, then artillery and then motorized rifle subunits. When the forward detachment approaches the river the artillery occupies positions 3-4 km from the river, while tanks and part of the artillery, especially anti-tank artillery and guided missiles move directly to the river bank, occupy positions for direct fire against the enemy weapons on the far bank. The action of the forward detachment and advance guards is supported by the artillery of the main body from positions located 5-km from the river.

The division establishes a forward command post at a vantage point to observe the action on the main direction for crossing. It crosses to the far bank with the first echelon regiments. The rear services move and cross as follows:
----- first echelon of regimental rear services are behind the first echelon battalions;
----- the second echelon of regimental rear services are behind the second echelon of the regiment;
----- the first echelon of the division rear services is behind the first echelon regiments;
----- the second echelon of the division rear services is behind the division second echelon.

Tactical and technical characteristics of the PMP ponton bridge park: it is designated to build pontoon crossing sites. One set requires 36 vehicles. From one set the following structures can be set up:
----- one bridge with a load capacity of 20 tons and length of 382 meters (built in 30 min);
----- one bridge with a load capacity of 60 tons and length of 227 meters (built in 50 min);
----- two bridges with lengths of 119 meters each;
----- or 16 ferries (rafts) with a load capacity of 40 tons; in 8 minutes;
----- 10 ferries (rafts) with load capacity of 60 tons; 10 minutes;
----- 8 ferries (rafts) with load capacity of 80 tons; in 12 minutes;
----- time for dismantling the bridge is 10-15 minutes.

Pontoon-bridge regiment of an army establishes army crossing sites on a water obstacle. In one hour the regiment can set up the following:
----- one 60-ton bridge with a length of 443 meters or;
----- one bridge with a load capacity of 20 tons, length of 760 meters or;
----- 20 ferries (rafts), each having a 60 ton load capacity or;
----- 16 ferries (rafts), each with a load capacity of 80 tons or;
----- 12 ferries (rafts), each with a load capacity of 110 tons.

An assault crossing battalion is normally given to first echelon divisions, or the battalion remains in the reserve of the army. The battalion can cross two tank companies or up to one and one half artillery batteries with their towing vehicles.


Miscelaneous Engineer Norms
Foxholes, trenches and cut and cover shelters reduce penetrating radiation 10 fold and decrease the radius of destruction by shock waves by 1.5 to 2 times. Shelters and dugouts with special engineer preparation reduce the radius of destruction to personnel by shock waves 3-5 fold.
The average daily standard consumption of water by one serviceman in areas which have little water or no water in the torrid zone such as in Central Asia or in Africa amounts to 10 liters. During an emergency shortage of water, the daily standard for water consumption can be reduced to 4 liters, but for a time period of no more than 3 days. Ths standards for consumption of water for technical purposes are dermined by the technical specifications of the type of vehicle. 2-4 water supply points are built for each regiment, moreover wells are dug in and at the CP's.


Engineer Planning Calculations

The following formulas and tables for performing calculations on engineer work were provided as typical samples in the basic Soviet book on tactical calculations (Vayner). Many others could be devised, but they would not vary much from standard American practice. Readers can refer to Soviet handbooks on engineers.



Calculating the Duration of a Water Crossing (or any obstacle)

According to the Soviet book on tactical calculations and the British derivative of it, this is the procedure for determining the time required to move an entire force accross an obstacle. The initial data required for the calculation is: the total number of vehicle trips required, the number of crossing vehicles available, and the time required for one trip.

The formula for the calculation:

where:
t=Duration of the total crossing in mins;
M=Required number of vehicle trips;
t_p=Duration of one trip;
N=Assigned number of crossing vehicles.

Example calculation given in the text:

Determine the length of time required for crossing 168 trucks when they can be carried 2 to a ferry. The time to cross each wave is 15 min and there are 24 amphibious crossing means. Dividing 168 by 2 indicates that 84 vehicle crossings are required. This times 15 min per crossing divided by 24 crossing vehicles at a time yields 52 minutes, the Soviet and British answer. However, on closer inspection it can be seen that 24 crossing means will require 3.5 trips to complete 84 crossings. Since this must be rounded up to 4 full cycles, we conclude that the correct answer is 4 times 15 or 60 minutes.

Examples of calculations using a nomogram.
1 Determine the crossing time for equipment when 88 vehicle crossings by crossing equipment are required to complete the lift, the crossing time is 12 minutes and the number of pieces of crossing equipment is 15. For the calculation draw a perpendicular line from the "88" mark on the scale of required number of crossings to the intersection with the "Crossing time=12" line.

Figure 1 - Nomogram to calculate time for crossing water obstacle with ferrying equipment

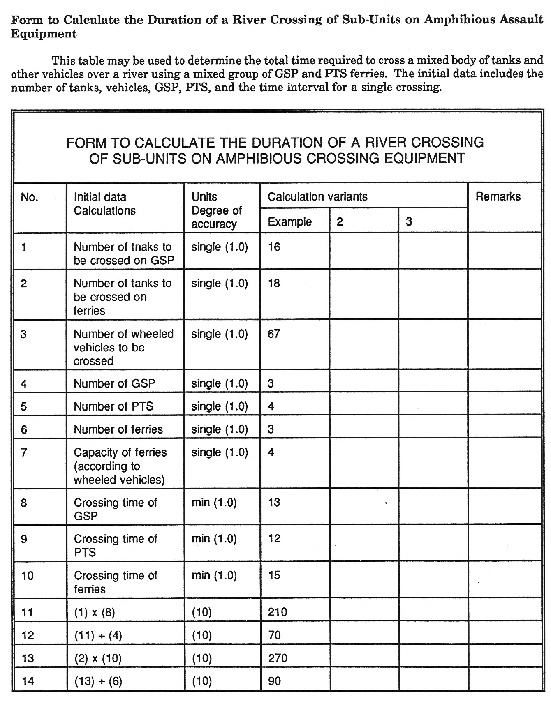
Figure 2 -Form to Calculate the Duration of a River Crossing of Sub-Units on Amphibious Assault Equipment

This table may be used to determine the total time required to cross a mixed body of tanks and other vehicles over a river using a mixed group of GSP and PTS ferries. The initial data includes the number of tanks, vehicles, GSP, PTS, and the time interval for a single crossing.

Duration of Water Crossing of Tanks in a Deep Ford or Submerged

The initial data for this calculation is the number of tanks or the required crossing time, and the data about the width of the river and time of day.

The formula is:

where:
t=time of crossing (min);
D=river width (m);
N=# of tanks;
d=spacing between tanks;
0.06=hr to min conversion;
V=tank underwater speed;
n=# of underwater routes;

Example: Determine the time required to cross 18 tanks in single file across a water obstacle 280 meters wide when the distance between vehicles is 60 meters and the vehicle travel speed during the crossing is 8 km per hr.
Solution: t=(280 + 18.60) x 0.06 ÷ 8=10 min

Determine how many tanks can cross a river 360 meters wide in 25 minutes in a single file when the tank travel speed is 6 km per hr and the distance between vehicles is 120 meters.

Solution: N=(25 x 6) - (0.06 x 360) ÷ (0.06 x 120)=18 tanks.

Examples using the nomogram: Determine the crossing time for 15 tanks under water along a single route at night accross a water obstacle 300 meters wide. Solving the problem is shown in variant a. Connect the 300 mark on the "River width" scale and the 15 mark on the "Number of tanks - night" scale and continue the line straight to the intersection with the "Crossing time along one route" scale, on which the answer shows as 18 minutes.

Determine how many tanks may cross a river 250 meters wide under water during the day along a single route in 15 minutes. In this calculation (variant b) connect the 250 mark on the "River width" scale and the 15 mark on the "Crossing time along one route" scale and at the intersection point with the "Number of tanks in day" scale read the answer is 25 tanks.

Figure 3 - Nomogram to calculate tank crossing under water.

Duration of a Crossing with one Ferry

The length of time required for a ferry or amphibious vehicle to cross a water obstacle depends on the character of the obstacle and the vehicle as well as the time required for loading and unloading. The initial data required for the calculation is the width of the river, speed of the current, speed of movement of the ferry equipment and the time required for the loading and unloading of cargo.

The formula is:

where:
- t=time of crossing in minutes;
- D=river width in meters;
- V=speed of travel in meters / min;
- V_f=current velocity meters/sec;
- t₁=time required for loading and unloading supplies;

Example: Determine the crossing time for water crossing equipment whose travel speed afloat is 8 km per hr (133 meters per min) when the width of the river is 360 meters, the current velocity is 2.5 meters per sec. and the loading and unloading time is 12 min.
Solution: t=(2 x 360 ÷ 133) (1 + (0.3 x 2.5)) + 12=22;

Example calculation using nomogram:

Determine the crossing time for water crossing equipment whose afloat speed is 9.5 km per hr (160 meters / min), when the river width is 250 meters, the current velocity is 2 meters/sec and the time for loading and unloading is 6 min.
Solution: Place a perpendicular line from the "250" point on the "River width" scale to the intersection with the "Currrent speed=2" line and from there move left along a horizontal line to the intersection with the "Water crossing equipment travel speed=160 line" and then drop a perpendicular line to the axis and mark the intersection point. Then draw a straight line through this point and the 6 mark on the "Loading and unloading time" scale to the intersection with the "Crossing time" scale on which the answer shows as 11 minutes.

This information can be used to determine total crossing time. For instance, if 15 crossings are required to cross the entire unit then the time will be 165 minutes.

Figure 4 - Nomogram for calculating duration of crossing a water obstacle

Figure 5 - Form for Calculating Manpower and Equipment, Necessary for the Construction of an Engineer Fortification

To use this form the planner enters the type of engineer construction work in column 2 and the number of each in column 3. He enters the standard norms for construction times in man days and machine hours as found in engineer reference works in columns 4 and 5. Some samples are provided in this table. Multiplication of column 3 by either 4 or 5 yields the entries for columns 6 and 7. These are then totaled at the bottom of the form.

Example calculation using the table: Determine the required number of mean and equipment to erect in two days the following fortifications: 128 single trench for riflemen, 6 sector trenches, 15 machine gun trenches, 20 - 10 meter trenches, 4 1oomm gun pits, 3 122mm gun pits, 3 120mm mortar pits, 18 BTR pits, 1 pit for tank, 5 OP's 3 open slit trenches, 4 sections of covered trench, 4 shelters, cover for 6 GAZ-69, cover for 4 ZIL-157, and cover for 5 BTR.
Solution: Enter the given data in the cells and perform the calculations as shown:

Calculation of the Number of Mines Required to Emplace a Mine Field

The initial data for this calculation is the extent of the area that must be covered with mines, the desired density of mines, and the density of the mine field.

The formulas are:

where:
- N=required number of mines to construct obstacles;
- D=width of front of feature to be covered with mines;
- P=density of obstacle (extent of mine field in km per km of front or %);
- n=density of mines (number of mines per km of minefield or %).

Example: Determine the number of mines required for mine fields accross an area 9.6 km wide with a density of mine fields of 0.85 (850 meters of minefield per 1 km of front) and a density of mines of 750 mines per km of minefield.
Solution: N=9.6 Km x 0.85 x 0.750 (750 mines per Km of mine field); 850 meters of mine field per Km of frontage=6120 unit

Determine the extent of an area which it is possible to protect by mine fields having available 2850 mines. The required density of mines is 0.75
Solution: D=2850 ÷ (750 x 0.75)=5 Km

Determine the density of mine fields on an area of 7.5 km width, if the expenditure of 4780 mines in a density of mines of 800 per km of minefield.
Solution: P=4760 ÷ (7.5 x 800)=0.8

Examples using the nomogram: Determine the required number of mines for the protection by mined obstacles of an area 6.5 km long, if the obstacle density is 0.6 and the density of mines is 700 per km of front. Solution: Variant a=2730 mines.

Determine the length of a feature which is to be protected by minefields with an availability of 3000 mines, if the density of mines is 600 per km of minefield and the obstacle density is 0.7.
Solution: Variant b=frontage of 7.1 km

Determine the density of minefields on an area 8.5 km wide if 3400 mines are available in a density of 800 mines per km of mine field.
Solution: variant a=0.5 km of obstacles per km of the area.

Figure 8 - Nomogram for calculating mine fields

Transportation planning factors

Calculation of the Necessary Amount of Transport for Moving Loads in a Set Time

Formula for Calculation:

where:
- N_P=Required number of vehicle sorties.
-P=Overall mass of load - tons.
-K=Coefficient of transportability.
-q=Load carrying capacity of vehicles - tons.
-t_P=Duration of one sortie - hours.
-D=Range of transportation - km.
-V=Average vehicle speed of movement - kph.
-t_nB=Time of loading/unloading.
-t_pass=Dead time.
-K_P=Number of sorties in a laid down time.
-T=Laid down time of transportation - hours.
-N=Required number of vehicles.

Example using the table: Determine the required number of vehicles to transport 42.5 tons over 65 km in 14.5 hours, it the coefficient of transportability is 1.25, the speed of vehicles is 30 km per hr, the vehicles have a capacity of 2.5 tons, the duration of loading and unloading time is 30 min and the dead time on each trip is 2 hrs.
Solution: Enter the given data in the table in the cells indicated and perform the arithmeticf. With a spread sheet or automatic form the results will appear automatically. The answer is shown in line 15 as 11 vehicles.

Table 112. Form for the Calculation of the Necessary Amount of Transport for the Transportation of Loads in a Set Time.

Figure 7 - Form to complete calculation of transportation requirement

Calculation of the Duration of Time to Move Loads by a Given Number of Vehicles

This set of formulas is essential similar to the last group. The purpose of the calculation is reversed.

Formula for Calculation:

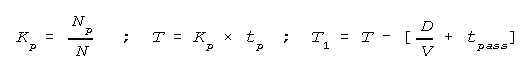
where:
- N_p=Required number vehicle trips;
- P=Overall weight of loads to be transported - tons;
- K=Coefficient of transportability of loads;
- q=Load carrying capacity of vehicles - tons;
- t_p=Duration of one move - hours;
- D=Distance of move - km;
- V=Average speed of vehicle movement - kph;
- t_{n x B}=Duration of loading/unloading of vehicles - hours.
- t_pass=Dead time (time for refuelling, technical maintenance, drivers rest period after each trip);
- K_P=Number of trips for each vehicle;
- N=Available assigned number of vehicles;
- T=Duration of move of loads with return of transport;
- T₁=Duration of transportation of loads without return of transport.

Example of the calculation using the table: Determine the duration of time required to transport 38.5 tons by 12 vehicles of 3 tons capacity over a distance of 85 km, when the coefficient of transportability is 1.5, the vehicle speed is 25 km per hr, the load and unload time is 30 min, and the dead time is 1 hr. Fill in the given data in the squares designated and use the table to keep track of the calculation. The time required is 16.6 hrs. To calculate the time requried without the vehicles returing from the last trip, subtract the duration of the return trip and dead time. This is shown in the table and the result is 12.2 hrs.

Figure 8 - Table for Calculating Time Required to Transport a Given Load with a Fixed Number of Vehicles

Calculation of Time Taken to Transport Sub-Units by Rail

An important calculation for strategic and long distance movement, such as reenforcements moved from the USSR to Germany.

Formula for calculation:

where.

- t=Time of troop transportation by rail - hours.
- D=Length of railway route - km.
- V=Average train speed - kpm.
- N=Number echelons to be transported.
- n=Rate of transportation (from loading conditions and character of railway route), trains - 24 hours.
- 24=Coefficient of conversion 24 periods to hour.
- D₁=Distance of FUP/concentration area to station - km.
- V₁=Average speed of movement from concentration area to station - kph.
- D₂=Distance from unloading station to new concentration area - km.
- V₂=Average speed of movement to new concentration area from unloading station _ kph.
- t=Time in organising transportation - hours.

Figure 9 - Table for calculating duration of railroad movement for sub-units

Example: using the table to organize daa when making calculations

Number of Aircraft (Helicopters) to Transport Loads

The basic data needed to calculate the number of aircraft is the weight of the transportable load, their transportability, the useful load capacity of the aircraft (helicopters) allotted for the transportation, length of air route, speed of the flight; and the time, necessary for technical maintenance, refuelling, and rest of crews between sorties.

The formula for the calculation:

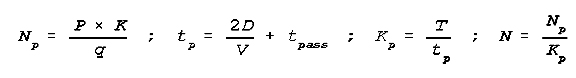
where:
- N_P=Required number of aircraft (helicopters) sorties transportation of loads (ordered op).
- P=Overall weight of loads - tons.
- K=Coefficient of load transportability in relation to the useful load carrying capacity of the aircraft (helicopters). The size of K is always greater or equal to 1. For example if the useful load carrying capacity of an aircraft is 8 tons, then into it, it is possible to load only 5 tons of cargo (because of its character, dimensions, volume - of the load and dimension of the air force), then the coefficient of transportability of a given type of aircraft will by 8:5=1.6.
- q=The useful load carrying capacity of the aircraft (helicopter) in given circumstances - ton. t=Duration of one sortie - hours;
- D_P=Range of transportation - km;
- V=Average speed of flight - kph;
- t_pass=Dead time (average time, necessary for loading, carloading, technical maintenance, refulling, etc., for one sortie);
- K_P=Number of sorties, which may be undertaken by aircraft in a prescribed time;
- T=Prescribed time.
- N=Required number of aircraft (helicopters) of transportation of loads in a given period (ordered op).

Example of the calculation using the table: Determine the number of aircraft required to lift 38 tons if the carryuing capacity of each aircraft is 12 tons, the coefficient of transportability is 1.5, the length of the move is 820 kms, the average flight speed is 700 km per hr, the dead time is 3 hrs and the time available for the move is 6 hrs.
Solution: Entering the given data in the table and performing the indicated calculations gives the answer that the lift requires 5 aircraft.

Figure 10 - Form to Calculate the Required Number of Aircraft

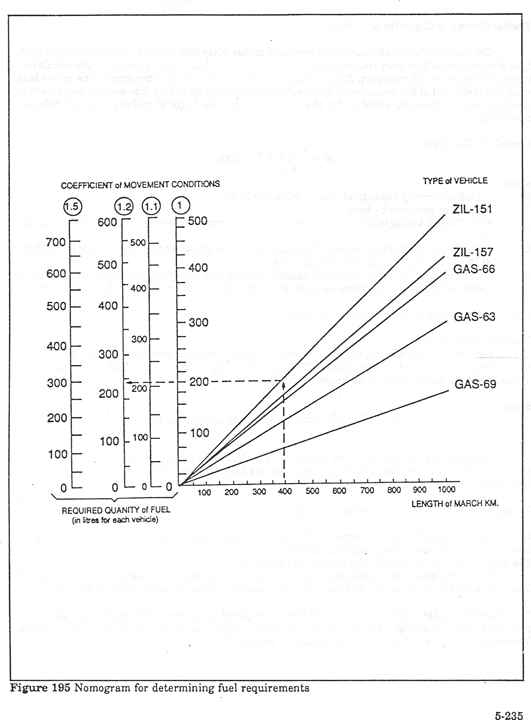
Calculation of Fuel Requirements for Selected Vehicles on march

This formula and nomogram are useful for quickly determining the fuel requirements for large numbers of vehicles to complete long marches. The nomogram is designed for the ZIL 157, ZIL 151, GAZ 66, GAZ 63, and GAZ 69 trucks. Similar nomograms could be developed for more modern vehicle types by using their standard fuel consumption characteristics. The initial data for the calculation are the route length, data about the type of vehicle, and the coefficient characterizing the travel conditions (road conditions, weather, season, time of day, etc). The basic formula is:

Q=D x n x K/ 100 x N

Where:

Q=required amont of fuel in liters:
D=length of march route in km:
n=norm of fuel consumption in liters/100 km;
K=coefficient introduced for march conditions
N=number of vehicles of the given type

Example calculations: Determine the required quantity offuel for 75 vehicles to compolete a 150 km march when teh fuel expenditure norm is 35 liters per 100 km and the travel conditions coefficient is 1.2.
Solution using formula is (150 x 35 x 1.2 x 75) / 100=4725 liters.
Example calculation using nomogram - determine the fuel expenditure for 35 ZIL 157 trucks for a 400 km march when the travel condition coefficient is 1.2.
Soluton: Draw a perpendicular line from the '400' mark on the 'Length of march' scale to the intersection with the 'ZIL 157' line. From this intersection draw a horizintal line to the left to intersect the 'Coefficient of movement conditions 1.2' line. At the point of intersection read the result of 240 liters per vehicle. Multiply by 35 vehicles to obtain 8400 total liters of fuel required.

Nomogram for determining fuel requirements

Traffic Carrying Capacity of a Route

Calculation of the traffic carrying capacity of routes takes into account: the quality of the road, type of movement of transport and conditions of movement. The basic data required for the calculation is speed of movement of transport, distance between vehicles, character of movement, one or two lane road, the coefficient of the reduction of the traffic carrying capacity taking into account movement in columns, and coefficients, allowing for the interaction on the route of railway lines of different capacities.

Formula to Calculate:

where.
- N=Traffic carrying capacity of road, vehicle per hour;
- V=Speed of movement - kph;
- q=Coefficient, taking into account the influence of returning movement in a two lane movement (1.6);
- k=Coefficient, taking into account the intensity of train movement (30 steam trains in 24 hrs - 0.75; 40 - 0.65; 50 - 0.57; 60 - 0.5; 70 - 0.4);
- K=Coefficient of lowering the traffic capacity taking into account of movement in columns in speeds of 10 km/hr - 2.8; 20km/hr - 2.4; 25 km/hr - 2.2; 30km/hr - 2; 40 km/hr - 1.8; 50 km/hr - 1.6;
- 1000=Coefficient for converting km to meters.

Example of calculation: Determine the traffic capacity of a section of route given that permitted speed - 30 kph, two lane movement, distance between vehicles 75m, route is cut by a railway main line with an intensity of movement 50 steam trains in 24 hours

Solution:




Reducing the distance between vehicles to 25m increases the traffic capacity to 546 vehicles per hour. Without the railway crossing, then under the same conditions the traffic carrying capacity is increased to 960 vehicles per hour.

Examples of calculation using nomogram.

l. Determine the traffic carrying capacity of a road with single lane movement if the permitted speed is 40 kph and distance between vehicles is 30m.
The nomogram a gives 740 vehicles per km in variant A.

If it is necessary to include the effect of a railway on the above example with, say, a rail intensity of 40 steam trains per 24 hours then the vehicle carrying capacity drops to 480 per km.

2. Determine what interval between vehicles is required to achieve 400 vehicles per km if the permitted speed on a single lane road is 30 kph, with a railway crossing with 30 trains in 24 hours. The nomogram gives not more than 28 meters in variant B.

Figure 11 - Nomogram to determine traffic capacity of a route